Колко лотарийни билета трябва да си купиш, за да си гарантираш печалба от Националната лотария? Отговорът дават математиците от университета на Манчестър, Великобритания.
Фокусирайки се върху водещата игра „Лото“, която тегли шест случайни числа от 1 до 59, д-р Дейвид Стюарт и д-р Дейвид Къшинг установяват, че 27 е най-малкият възможен брой билети. Учените обаче правят уточнение, че все пак няма гаранция за голяма печалба.
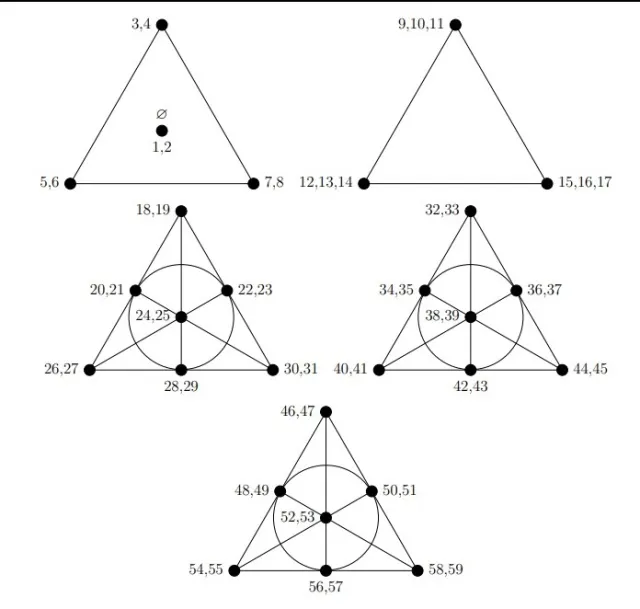
Те описват математическа система - наречена крайна геометрия, която е фокусирана около триъгълна структура (равнината на Фано). Всяка точка от структурата е начертана с двойки числа и е свързана с линии - всяка линия генерира набор от шест числа, което се равнява на един билет, съобщава BBC News.
Необходими са три равнини на Фано и два триъгълника, за да се обхванат всички 59 числа и да се генерират 27 комплекта билети. Избирането на билети по този начин гарантира, че независимо от това кое от 45 057 474 възможни тегления се случи, поне един от фишовете ще има две съвпадащи числа.
Любопитен е факта, че през юли във Великобритания има петима нови милионери. Един е спечелил над 11,6 млн. паунда, а другите четирима – над един милион. Тези големи суми са рядкост, но много хора се радват на по-дребни печалби.
По този повод германското издание „Шпигел“ съобщава, че вероятността в страната да бъде спечелена сума над един милион от лотария е 1 към 140 милиона. А вероятността да се удари шестица от тотото в България е 1 към близо 14 милиона, твърдят родни математици.